如何理解1x1卷积？1x1卷积为什么可以降维？

1x1卷积就是卷积核大小为1x1的卷积操作。1x1卷积操作的目的很明确：就是变维（这里的维度是指channels维度的数量，而不是增加或者减少特征维度，这个计算机领域的遣词还是要多打磨啊，不然会很误导）。因此1x1卷积也可以被看作一种全连接层，因为达到了类似的操作和类似的效果。这里对1x1操作具体地进行分析，以助理解。

之前看到网上介绍1x1卷积的各种图，感觉都很抽象，每次都要想半天，所以这篇文章好好捋一捋！

CNN中的channels和多filter

首先，得先复习一下CNN的一些基础的概念，这样才能更好地理解1x1卷积。

CNN中的channels有两种（或者说三种）：

• in_channels: 输入卷积层的channels数量，取决于上一层的out_channels；如果是第一层，那就是输入图像本身的channels，比如RGB三通道图像。
• out_channels: 卷积层输出的channels数量，取决于卷积核(filter)的个数。

为什么out_channels取决于卷积核的个数呢？因为一个卷积核本质上会综合全部的输入通道，然后输出一个通道。那么输出了多个通道的特征图的卷积层，本质上是由于多个卷积核各自输出了一张特征图。因此，有多少个filter就会产生多少个out_channels。这很重要！千万不要在学习的过程中忽略这点！

也就是说每个卷积核只会产生一张特征图，但是它的信息其实是采样自每一个输入通道的！这里我贴一张引用的别人的博客的图片辅助理解：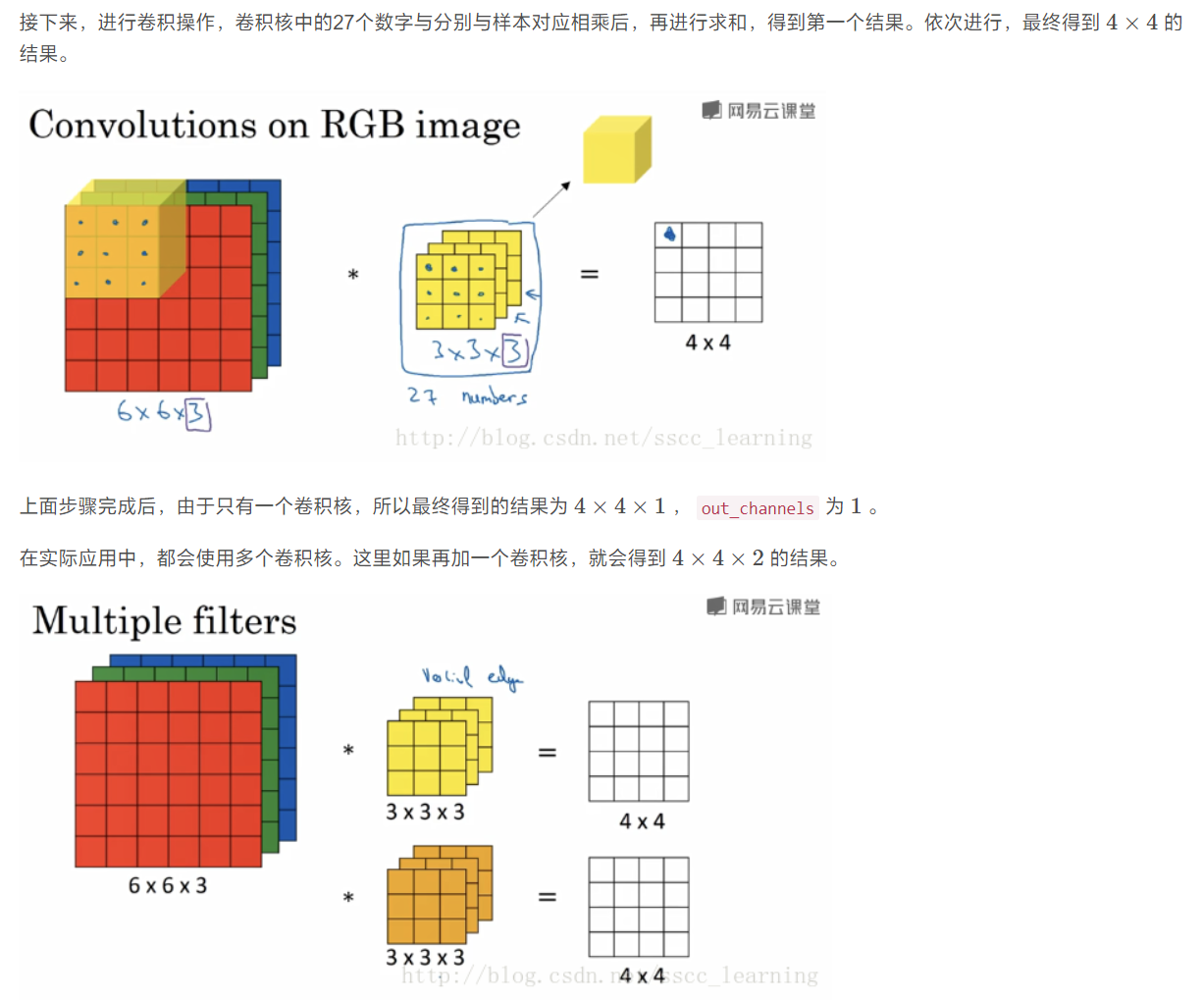

1x1卷积

1x1卷积核最早出现在NIN的论文中。有两个用处：①变换维度——其实这里指的是变换了channels维度的数目，并且虽然我们说1x1卷积可以用于降维，但是其实保持channels维度的数目不变或者升高channels维度的数目也是可以的。②增加神经网络的非线性——这样做可以跨通道地进行信息整合。

那么1x1卷积是如何做到的呢？如下图所示，首先对于一张特征图和一个1x1x1的卷积核来说，并不会对特征图的width和height产生影响，所做的操作只是线性变换。
而，对于多个channels的输入特征（如图6x6x32），经过一个卷积核(如图1x1x32)的操作之后，就变成了6x6x1的输出特征图；如果此时，假设有m个1x1x32的卷积核进行卷积操作，那么输出的维度就是6x6xm。也就是上面我们复习的，**每个1x1x32的卷积核其实都综合了每个输入通道（总共6x6x32）的信息得到了一张6x6x1的特征图，这m个卷积核的操作加起来，得到了最终的输出——6x6xm**。所以1x1卷积也可以看作类似全连接操作，因为每个卷积核都连接了每个channel，就像全连接层里的一排的任意个数的neuron。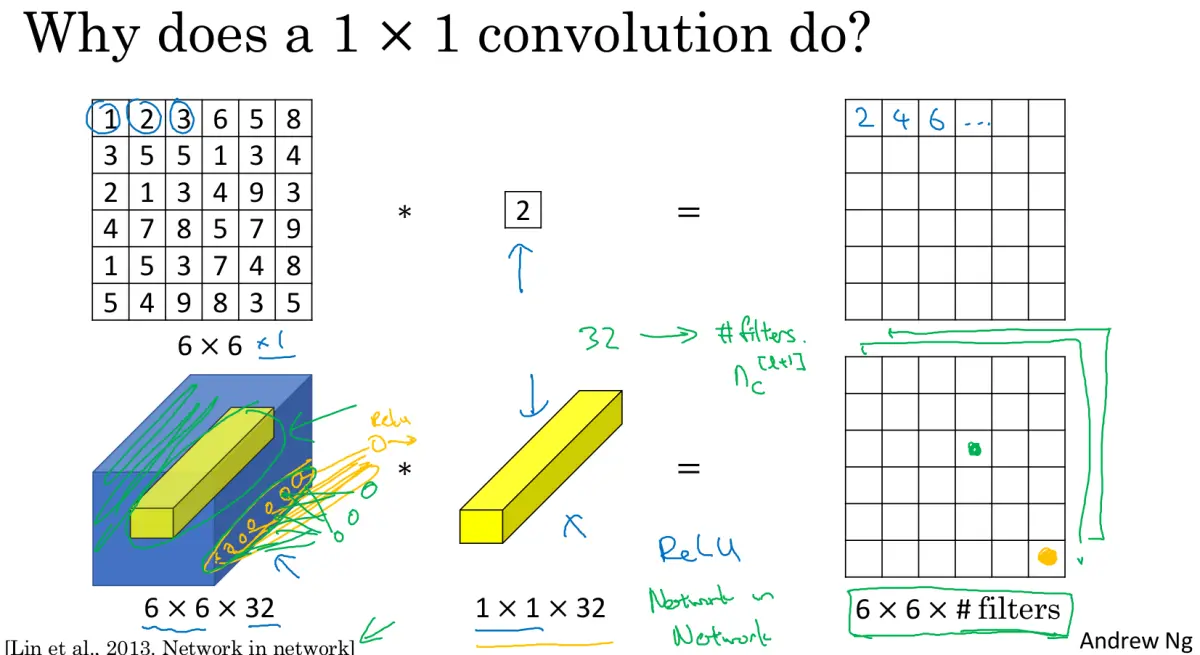

这就是为什么1x1卷积可以变维：我们给出几个卷积核，就能得到几个channels的输出特征图；并且这些卷积核会去综合每个channel的信息。
这个时候再看这张图，就十分清晰并且可以理解了：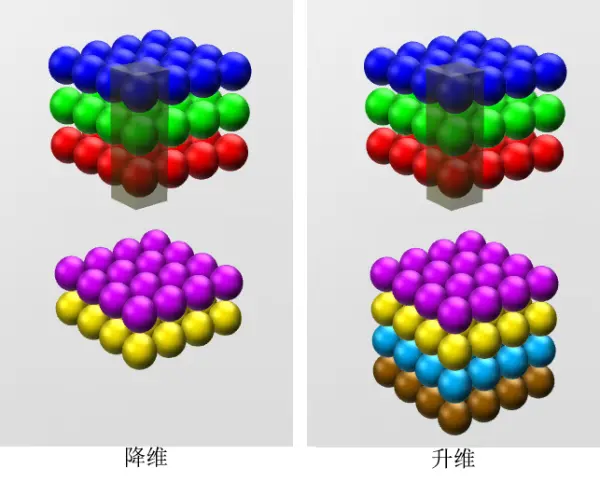

References

卷积神经网络中用1*1卷积有什么作用或者好处呢？ - 简书
Network in network - arxiv
【CNN】理解卷积神经网络中的通道 channel - CSDN